Connaître le parallélépipède rectangle
Introduction :
L’objectif de ce cours est de connaître le parallélépipède rectangle.
Dans un premier temps, nous représenterons en perspective cavalière un parallélépipède rectangle pour observer ses propriétés. Dans un deuxième temps, nous verrons les patrons de parallélépipède rectangle et, enfin, nous donnerons la formule permettant d’obtenir le volume d’un parallélépipède rectangle.
Représentation d’un parallélépipède rectangle en perspective cavalière
Représentation d’un parallélépipède rectangle en perspective cavalière
Qu’est-ce que la perspective cavalière ?
Qu’est-ce que la perspective cavalière ?
Dans une représentation en perspective cavalière :
- les faces avant et arrière sont représentées en vraie grandeur ;
- les segments (ou droites) et plans parallèles restent parallèles ;
- les segments parallèles et de même longueur restent parallèles et de même longueur ;
- seuls les angles droits des faces avant et arrière sont représentés par des angles droits ;
- les longueurs des arêtes qui n’appartiennent pas aux faces avant et arrière sont réduites ;
- les arêtes cachées sont représentées en pointillés.
Définition
Face :
Une face est une surface plane d’un solide.
Définition
Arête :
Une arête est un segment commun à deux faces d’un solide.
Définition
Sommet :
Un sommet est une extrémité d’une arête d’un solide.
Qu’est-ce qu’un parallélépipède rectangle ?
Qu’est-ce qu’un parallélépipède rectangle ?
Définition
Parallélépipède rectangle :
Un parallélépipède rectangle est un solide dont les $6$ faces sont des rectangles et dont les faces opposées sont des rectangles de mêmes dimensions.
Le solide $ABCDEFGH$ représenté ci-dessous en perspective cavalière est un parallélépipède rectangle : toutes ses faces sont rectangulaires et ses faces opposées sont des rectangles de mêmes dimensions.
Le parallélépipède rectangle $ABCDEFGH$ a :
- $8$ sommets : ce sont les points $A$, $B$, $C$, $D$, $E$, $F$, $G$ et $H$ ;
- $6$ faces : les rectangles $ABCD$, $EFGH$, $ABFE$, $DCGH$, $AEHD$ et $BFGC$ ;
- $12$ arêtes : les segments $[AB]$, $[EF]$, $[HG]$, $[DC]$, $[AD]$, $[EH]$, $[BC]$, $[FG]$, $[AE]$, $[BF]$, $[CG]$ et $[DH]$.
À retenir
Un parallélépipède rectangle a $3$ dimensions qui sont les longueurs de $3$ arêtes qui ont un sommet commun.
Pour le parallélépipède rectangle $ABCDEFGH$, ce pourrait être les longueurs $AB$, $AD$ et $AE$.
Astuce
Un parallélépipède rectangle est aussi appelé pavé droit.
À retenir
Si les $6$ faces d’un parallélépipède rectangle sont des carrés, alors c’est un cube.
Propriétés du parallélépipède rectangle
Propriétés du parallélépipède rectangle
Propriété
Un parallélépipède rectangle a ses faces opposées superposables et parallèles.
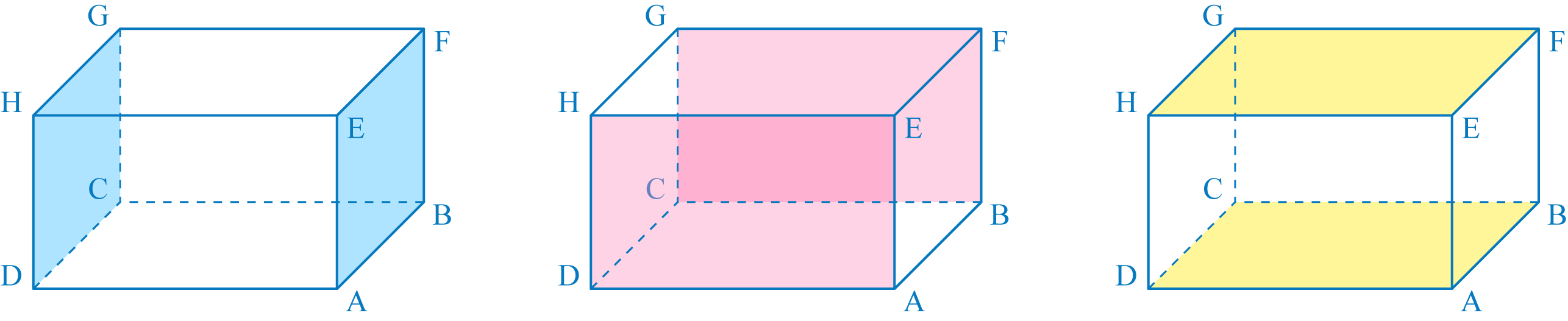
- Par exemple, les faces $ABFE$ et $DCGH$ sont superposables et parallèles.
Propriété
Un parallélépipède rectangle a ses faces consécutives perpendiculaires.
- Par exemple, les faces $ABFE$ et $EFGH$ sont perpendiculaires.
Propriété
Un parallélépipède rectangle a des arêtes opposées parallèles et de même longueur puisque les faces sont des rectangles.
- Par exemple, les arêtes $[AB]$ et $[EF]$ sont parallèles et de même longueur.
Propriété
Un parallélépipède rectangle a des arêtes issues d’un même sommet perpendiculaires puisque les faces sont des rectangles.
- Par exemple, les arêtes $[CG]$ et $[GH]$ sont perpendiculaires.
Patron d’un parallélépipède rectangle
Patron d’un parallélépipède rectangle
Définition
Patron d’un solide :
Un patron d’un solide est une figure plane qui permet, après pliage, de fabriquer exactement, sans superposition, ce solide.
Patron d’un parallélépipède rectangle
Patron d’un cube
Volume d’un parallélépipède rectangle
Volume d’un parallélépipède rectangle
À retenir
- Les longueurs $AB$, $AD$ et $AE$ sont les $3$ dimensions du parallélépipède rectangle $ABCDEFGH$.
- Si $AD = a$, $AB = b$ et $AE = c$ ($a$, $b$ et $c$ exprimées dans les mêmes unités), le volume $V$ du parallélépipède rectangle est : $$V = a\times b\times c$$
- Si $ABCDEFGH$ est un cube, et donc que $AD = AB = AE = a$, alors le volume de ce cube est : $$V = a\times a\times a = a^3$$
Conclusion :
Dans ce cours, nous avons vu une façon simple de représenter un parallélépipède rectangle qui est la représentation en perspective cavalière.
À l’aide de cette représentation, nous avons pu observer qu’un parallélépipède rectangle a $8$ sommets, $6$ faces rectangulaires et $12$ arêtes.
Si les $6$ faces de ce parallélépipède rectangle sont des carrés, alors c’est un cube.
Nous avons ensuite vu que nous pouvions tracer un patron d’un parallélépipède rectangle, c'est-à-dire tracer une figure plane qui permet, après pliage, d’obtenir ce solide sans superposition des faces.
Nous avons enfin vu la formule donnant le volume d’un parallélépipède rectangle qui est le produit de ses trois dimensions.