Géométrie repérée

Colinéarité de deux vecteurs

Définition

Définition

Colinéarité de deux vecteurs

On considère $\vec u$ et $\vec v$ deux vecteurs non nuls.

Les vecteurs $\vec u$ et $\vec v$ sont colinéaires si et seulement si l’un est le produit de l’autre par un réel, c’est-à-dire s’il existe un réel $k$ tel que $\vec v=k\vec u$.

Le réel $k$ est le coefficient de colinéarité. Ainsi, deux vecteurs non nuls sont colinéaires lorsqu’ils ont la même direction.

À retenir

Par convention, $\vec 0$ (le vecteur nul) est colinéaire à tout vecteur.

Condition de colinéarité

Propriété

Condition de colinéarité

Soit $\vec u\begin{pmatrix} x \ y \end{pmatrix}$ et $\vec v\begin{pmatrix} x' \ y' \end{pmatrix}$ deux vecteurs donnés par leurs coordonnées dans un repère orthonormé du plan.

Les vecteurs $\vec u$ et $\vec v$ sont colinéaires si et seulement si leurs coordonnées sont proportionnelles, c’est-à-dire uniquement si $xy'-yx'=0$.

Applications de la colinéarité

Propriété

Deux droites $(AB)$ et $(CD)$ sont parallèles si et seulement si les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{CD}$ sont colinéaires.

Propriété

Trois points $A$, $B$ et $C$ sont alignés si et seulement si les vecteurs $\overrightarrow{AB}$ et ${\overrightarrow{AC}}$ sont colinéaires.

Vecteur directeur d’une droite et vecteur normal à une droite

Définitions

Définition

Vecteur directeur d’une droite

Soit $\mathscr D$ une droite et $\vec u$ un vecteur non nul du plan.

On dit que $\vec u$ est un vecteur directeur de $\mathscr D$ s’il existe deux points $A$ et $B$ de $\mathscr D$ tels que  $\vec u={\overrightarrow{AB}}$.

Vecteur directeur d’une droite

Propriété

Soit $\vec u$ un vecteur directeur d’une droite $\mathscr D$.

Le vecteur $\vec v$ est un vecteur directeur de la droite $\mathscr D$ si et seulement si le vecteur $\vec v$ est non nul et colinéaire au vecteur $\vec u$.

Définition

Vecteur normal à une droite

Soit $\vec n$ un vecteur non nul et $\mathscr D$ une droite.

On dit que $\vec n$ est un vecteur normal à $\mathscr D$ si $\vec n$ est orthogonal à un vecteur directeur de $\mathscr D$ ($\overrightarrow{AM}$, par exemple).

Vecteur normal à une droite

Parallélisme et vecteurs directeurs

Propriété

Propriété 

Soit $\mathscr D$ et $\mathscr D'$ deux droites de vecteurs directeurs respectivement $\vec u$ et $\vec v$.
$\mathscr D$ et $\mathscr D'$ sont parallèles si et seulement si $\vec u$ et $\vec v$ sont colinéaires.

Autrement dit, deux droites du plan sont parallèles si et seulement si les vecteurs directeurs de l’une sont colinéaires aux vecteurs directeurs de l’autre.

Caractérisation de l’appartenance d’un point à une droite

Propriété

Soit $A$ un point du plan, $\vec u$ un vecteur non nul et $\mathscr D$ la droite passant par $A$ de vecteur directeur $\vec u$.

Un point $M$ appartient à la droite $\mathscr D$ si et seulement si les vecteurs $\vec u$ et $\overrightarrow{AM}$ sont colinéaires.

Appartenance d’un point à une droite

• Dans les parties suivantes, le plan est muni d’un repère orthonormé $(O\ ;\,\vec\imath,\,\vec\jmath\,)$.

Équations de droites

Équations cartésiennes de droites

Propriété

Les coordonnées $(x\ ;\,y)$ de tous les points $M$ d’une droite $\mathscr D$ vérifient une équation de la forme $ax+by+c=0$, où $a$, $b$ et $c$ sont des réels, avec $(a\ ;\,b)\neq(0\ ;\,0)$.
Une telle équation s’appelle une équation cartésienne de $\mathscr D$.

• Dans ce cas, le vecteur $\vec u \begin{pmatrix} -b \ a \end{pmatrix}$ est un vecteur directeur de la droite $\mathscr D$ et le vecteur $\vec n \begin{pmatrix} a \ b \end{pmatrix}$ est un vecteur normal à cette droite.
• Réciproquement, pour $a$ et $b$ deux réels, $(a\ ;\,b)\neq(0\ ;\,0)$, si une droite $\mathscr D$ a pour vecteur directeur $\vec u \begin{pmatrix} -b \ a \end{pmatrix}$ ou pour vecteur normal $\vec n \begin{pmatrix} a \ b \end{pmatrix}$, alors elle admet une équation cartésienne de la forme $ax+by+c=0$, où $c$ est un nombre réel à déterminer.

Exemples

• Considérons une droite $\mathscr D$ passant par le point $A\,(-4\ ;\,7)$ et qui admet pour vecteur normal le vecteur $\vec n \begin{pmatrix} 2 \ 3 \end{pmatrix}$.
• On peut en déterminer une équation cartésienne.

$\vec n \begin{pmatrix} 2 \ 3 \end{pmatrix}$, alors $\begin{cases} a=2 \ b=3\end{cases}$.

Donc, $ax+by+c=0$ devient  $2x+3y+c=0$, où $c$ est un nombre réel à déterminer.

• On sait que $A(-4\ ;\,7)\in\mathscr D$, ce qui permet de calculer $c$.

$\begin{aligned} 2\times(-4)+3\times7+c=0&\Leftrightarrow-8+21+c=0 \ &\Leftrightarrow13+c=0 \ &\Leftrightarrow c=-13 \end{aligned}$

• Une équation cartésienne de $\mathscr D$ est donc  $2x+3y-13=0$.
• On souhaite déterminer une équation de la droite $\mathscr D$ qui admet pour vecteur normal $\vec n\begin{pmatrix} 1\3 \end{pmatrix}$ et passe par le point $A\,(2\ ; -1)$.
• On note $M\,(x\ ;\,y)$ un point de la droite $\mathscr D$.

Le vecteur $\overrightarrow{AM}$ est alors un vecteur directeur de $\mathscr D$.

$\overrightarrow{AM} \begin{pmatrix} x$M-xA \ yM-yA \end{pmatrix} =\overrightarrow{AM} \begin{pmatrix} x-2 \ y+1 \end{pmatrix}

• Comme $\vec n$ est un vecteur normal à $\mathscr D$, $\vec n$ est orthogonal à un vecteur directeur de $\mathscr D$.

$\begin{aligned} \overrightarrow{AM} \cdot \vec n=0&\Leftrightarrow(x-2)×1+(y+1)×3=0 \ &\Leftrightarrow x-2+3y+3=0 \ &\Leftrightarrow x+3y+1=0 \end{aligned}$

• Ainsi, $x+3y+1=0$ est une équation cartésienne de $\mathscr D$.
• On considère le point $A\,(1\ ;\,-2)$ et la droite $\mathscr D$ d’équation cartésienne $x+2y-7=0$.

On souhaite déterminer les coordonnées du point $H$, projeté orthogonal du point $A$ sur la droite $\mathscr D$.

• Le vecteur $\vec{n} \begin{pmatrix}1 \ 2 \end{pmatrix}$ est un vecteur normal à la droite $\mathscr D$, donc un vecteur directeur de la droite $\mathscr D'$ perpendiculaire à la droite $\mathscr D$ passant par le point $A$.

La droite $\mathscr D'$ admet donc une équation cartésienne de la forme  $2x-y+c=0$ ($c$ un nombre réel).

• $A\in\mathscr D'$, donc ses coordonnées vérifient l’équation cartésienne de $\mathscr D'$

$2\times 1 - (-2) + c = 4 + c = 0$, donc $c = -4$.

La droite $\mathscr D'$ admet donc pour équation cartésienne  $2x -y - 4 = 0$.

• Par définition, $H\,(x\ ;\,y)$ est l’intersection des droites $\mathscr D$ et $\mathscr D'$, donc ses coordonnées sont les solutions du système de 2 équations à 2 inconnues suivant 

$\begin{cases} x+2y-7&=&0 \ 2x-y-4&=&0 \end{cases}$

Résolvons-le 

$\begin{aligned} \begin{cases} x+2y-7&=&0 \ 2x-y-4&=&0 \end{cases} &\Leftrightarrow\begin{cases} x=-2y+7 \ 2x-y-4=0 \end{cases} \ &\Leftrightarrow\begin{cases} x=-2y+7 \ 2(-2y+7)-y-4=0 \end{cases} \ &\Leftrightarrow\begin{cases} x=-2y+7 \ -4y+14-y-4=0 \end{cases} \ &\Leftrightarrow\begin{cases} x=-2y+7 \ -5y=-10 \end{cases} \ &\Leftrightarrow\begin{cases} x=-2y+7 \ y=\frac{-10}{-5}=2 \end{cases} \ &\Leftrightarrow\begin{cases} x=-2\times2+7 \ y=2 \end{cases} \ &\Leftrightarrow\begin{cases} x=3 \ y=2 \end{cases} \end{aligned}$

• Le point $H$, projeté orthogonal du point $A$ sur la droite $\mathscr D$, a pour coordonnées $H\,(3\ ;\,2)$.

Équation d’un cercle

Définition

Équation de cercle

Soit $\mathscr C$ un cercle de centre $\Omega\,(x$\Omega\ ;\,y\Omega) et de rayon $R$.

Une équation cartésienne du cercle $\mathscr C$ est 

$(x-x$\Omega)^2+(y-y\Omega)^2=R^2

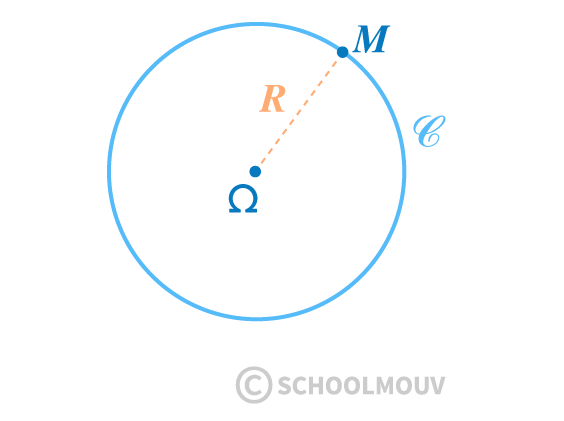
Réciproquement, $(x-x$\Omega)^2+(y-y\Omega)^2=R^2 est l’équation d’un cercle de centre $\Omega\ (x$\Omega\ ;\,y\Omega) et de rayon $R$.

Astuce

Le caractère grec $\Omega$ se lit oméga.

Comme nous l’avons vu dans la leçon sur le produit scalaire, il est possible de déterminer une équation cartésienne d’un cercle de diamètre $[AB]$ grâce au produit scalaire.

Propriété

Soit $A$ et $B$ deux points distincts.

L’ensemble des points $M$ tels que $\overrightarrow{MA}\cdot\overrightarrow{MB}=0$ est le cercle de diamètre $[AB]$.

Exemples

• Soit le cercle $\mathscr C$ de diamètre $[AB]$ avec $A\,(1\ ;\,1)$ et $B\,(5\ ;\,-2)$.

On souhaite déterminer une équation cartésienne de ce cercle.

Méthode 1

Pour trouver une équation cartésienne de ce cercle, on peut utiliser la propriété précédente 

$M\,(x\ ;\,y)$ appartient au cercle $\mathscr C$ si et seulement si $\overrightarrow{MA}\cdot\overrightarrow{MB}=0$.

Les coordonnées du vecteur $\overrightarrow{MA}$ sont 

$\overrightarrow{MA} \begin{pmatrix} x$A-xM \ yA-yM \end{pmatrix}=\overrightarrow{MA} \begin{pmatrix}1-x \ 1-y \end{pmatrix}

Les coordonnées du vecteur $\overrightarrow{MB}$ sont 

$\overrightarrow{MB} \begin{pmatrix} x$B-xM \ yB-yM \end{pmatrix} =\overrightarrow{MB} \begin{pmatrix}5-x \ -2-y \end{pmatrix}

$\begin{aligned} \overrightarrow{MA}\cdot\overrightarrow{MB}=0&\Leftrightarrow(1-x)\times(5-x)+(1-y)\times(-2-y)=0 \ &\Leftrightarrow 5-x-5x+x^2-2-y+2y+y^2=0 \ &\Leftrightarrow x^2-6x+y^2+y+3=0 \ &\Leftrightarrow (x^2-6x+9)-9+\Big(y^2+y+\dfrac{1}{4}\Big)-\dfrac{1}{4}+3=0 \ &\Leftrightarrow (x-3)^2-9+\Big(y+\dfrac{1}{2}\Big)^2-\dfrac{1}{4}+3=0 \ &\Leftrightarrow(x-3)^2+\Big(y+\dfrac{1}{2}\Big)^2=\dfrac{25}{4} \end{aligned}$

Méthode 2

Le cercle $\mathscr C$ de diamètre $[AB]$, avec $A\,(1\ ;\,1)$ et $B\,(5\ ;\,-2)$, est aussi le cercle de centre $I=\text{mil}\,[AB](\frac{1+5}{2}\ ;\,\frac{1-2}{2})$, c’est-à-dire  $I\,(3\ ;\,-\frac{1}{2})$.

Il a pour rayon $IA$ tel que 

$\begin{aligned} IA^2&=(1-3)^2+\bigg(1-\Big(-\frac{1}{2}\Big)\bigg)^2 \ &= {(-2)}^2 + \Big(1+\frac{1}{2}\Big)^2 \ &= 4 + \Big(\frac{3}{2}\Big)^2 \ &= 4 + \frac{9}{4} \ &= \frac{25}{4} \ &= \Big(\frac{5}{2}\Big)^2 \end{aligned}$

D’après la propriété, une équation cartésienne du cercle $\mathscr C$, de centre $I\,(3\ ;\,-\frac{1}{2})$ et de rayon $IA=\frac{5}{2}$, est 

$\begin{aligned} (x-3)^2+\bigg(y-\Big(-\dfrac{1}{2}\Big)\bigg)^2&=\Big(\dfrac{5}{2}\Big)^2=\dfrac{25}{4} \ (x-3)^2+\Big(y+\dfrac{1}{2}\Big)^2&=\dfrac{25}{4} \end{aligned}$

• On désigne par $\mathscr C$ l’ensemble des points $M\,(x\ ;\,y)$ tels que 

$x^2+y^2+2x-y -\dfrac{47}{4}=0$

On souhaite démontrer que $\mathscr C$ est un cercle, puis donner son centre et son rayon.

$\begin{aligned} M\,(x\ ;\,y)\in\mathscr C&\Leftrightarrow x^2+y^2+2x-y-\dfrac{47}{4}=0 \ &\Leftrightarrow x^2+2x+y^2-y-\dfrac{47}{4}=0 \ &\Leftrightarrow (x^2+2x+1)-1+\Big(y^2-y+\dfrac{1}{4}\Big)-\dfrac{1}{4}-\dfrac{47}{4}=0 \ &\Leftrightarrow (x+1)^2-1+\Big(y-\dfrac{1}{2}\Big)^2-\dfrac{1}{4}-\dfrac{47}{4}=0 \ &\Leftrightarrow (x+1)^2+\Big(y-\dfrac{1}{2}\Big)^2=\dfrac{52}{4}=13 \ &\Leftrightarrow \Omega M^2 = 13 = \sqrt{13}^2\ \text{avec}\ \Omega\,\Big(-1\ ;\,\dfrac{1}{2}\Big) \end{aligned}$

• $\mathscr C$ est donc le cercle de centre $\Omega\,(-1\ ;\,\frac{1}{2})$ et de rayon $R=\sqrt{13}$.

Équation cartésienne d’une parabole

Une parabole est la représentation graphique d’une fonction polynôme $f$ de degré $2$ définie sur $\mathbb{R}$ par $f(x)=ax^2+bx+c$, avec $a\neq0$, $b$ et $c$ trois nombres réels.
Une parabole a donc pour équation cartésienne $y = ax^2+bx+c$ avec $a\neq 0$, $b$ et $c$ trois nombres réels.

• Si $a>0$, $f$ est strictement décroissante sur $]-\infty\ ;\,-\frac{b}{2a}]$, puis strictement croissante sur $[-\frac{b}{2a}\ ;\,+\infty[$

$f$ admet un minimum $\beta$, atteint en $x= -\dfrac{b}{2a}$.

La courbe représentative de $f$ est une parabole de sommet $S$ de coordonnées $\big(\alpha = -\frac{b}{2a} \ ;\ \beta = f(-\frac{b}{2a})\big)$ et avec les branches tournées vers le haut.

Elle admet la droite d’équation $x = -\dfrac{b}{2a}$ comme axe de symétrie.

• Si $a<0$, $f$ est strictement croissante sur $]-\infty\ ;\,-\frac{b}{2a}]$, puis strictement décroissante sur $[-\frac{b}{2a}\ ;\,+\infty[$

$f$ admet un maximum $\beta$, atteint en $x=-\dfrac{b}{2a}$.

La courbe représentative de $f$ est une parabole de sommet $S$ de coordonnées $\big(\alpha = -\frac{b}{2a}\ ;\ \beta = f(-\frac{b}{2a})\big)$ et avec les branches tournées vers le bas.

Elle admet la droite d’équation $x = -\dfrac{b}{2a}$ comme axe de symétrie.