La fonction inverse
Introduction :
Tout comme la fonction carré qui fait l’objet d’un autre cours, la fonction inverse est une fonction de référence. Comme leur nom l’indique, ces fonctions servent de référence pour étudier les variations, les extrema et les représentations graphiques d’autres fonctions plus complexes.
Nous allons donc débuter cette leçon par la définition et les propriétés de la fonction inverse puis nous verrons comment résoudre des équations et inéquations grâce à cette fonction.
Fonction inverse
Fonction inverse
Définition
Définition
Définition
Fonction inverse :
La fonction qui à tout nombre réel $x$ non nul associe son inverse $\dfrac{1}{x}$ est appelée fonction inverse.
Elle est définie sur $]-\infty\ ;\,0[\,\cup\,]0\ ;\,+\infty[$ par $f(x)=\dfrac{1}{x}$.
Cet ensemble de définition se note aussi $\mathbb{R}\smallsetminus \lbrace 0 \rbrace$ ou $\mathbb{R}^*$ (qui se lit $\mathbb{R}$ privé de zéro)
Exemple
$f(2)=\dfrac{1}{2}=0,5$
$f(-3)=\dfrac{1}{-3}=-\dfrac{1}{3}$
$f\left(\dfrac{1}{5}\right)=\dfrac{1}{\frac{1}{5}}=5$
Représentation graphique et propriétés
Représentation graphique et propriétés
Pour tracer la courbe représentative de la fonction inverse, on établit son tableau de valeurs :
| $x$ | $-4$ | $-3$ | $-2$ | $-1$ | $-0,5$ | $0$ | $0,5$ | $1$ | $2$ | $3$ | $4$ |
| $\dfrac1x$ | $-0,25$ | $-\dfrac13$ | $-0,5$ | $-1$ | $-2$ | $2$ | $1$ | $0,5$ | $\dfrac13$ | $0,25$ |
- On voit par exemple dans ce tableau que l’image de $-4$ est $-0,25$ et que l’image de $1$ est $1$.
- On voit aussi que $0$ n’a pas d’image par la fonction inverse.
Courbe représentative d’une fonction inverse
- La courbe représentative de la fonction inverse est une hyperbole.
- La courbe représentative de la fonction inverse ne coupe pas l’axe des abscisses.
- Il n’y a aucun point d’abscisse $0$ sur la courbe de la fonction inverse puisque cette fonction n’est pas définie en $0$.
Propriété
La courbe représentative de la fonction inverse est symétrique par rapport à l’origine $0$ du repère. Pour tout réel $a$ on a : $$f(-a)=\dfrac{1}{-a}=-\dfrac{1}{a}=-f(a)$$
- Les deux points de coordonnées $A\left(a\ ;\ \dfrac{1}{a}\right)$ et $B\left(-a\ ;\ -\dfrac{1}{a}\right)$ sont donc symétriques par rapport à l’origine du repère.
Courbe représentative d’une fonction inverse
Propriété
La fonction inverse est décroissante sur l’intervalle $]-\infty\ ;\ 0[$ et décroissante sur $]0\ ;+\infty[$.
Son tableau de variation est le suivant :
- Dans le tableau de variation, la double barre sous le « zéro » permet de montrer que la fonction inverse n’est pas définie en $0$. On dit que $0$ est une valeur interdite.
- La propriété que nous venons de voir permet de comparer deux inverses :
Exemple
- $2<5$ donc $\dfrac{1}{2}>\dfrac{1}{5}$ car la fonction inverse est strictement décroissante sur $]0\ ;+\infty[$ et donc en particulier sur $[2\ ;\ 5]$ ;
- $-6<-3$ donc $-\dfrac{1}{6}>-\dfrac{1}{3}$ car la fonction inverse est strictement décroissante sur $]-\infty\ ;\ 0[$ et donc en particulier sur $[-6\ ;\ -3]$.
À retenir
La fonction inverse inverse l’ordre sur $]-\infty ;\ 0[$ et sur $]0\ ;+\infty[$ :
- si $0 < a < b$ alors $\dfrac1a>\dfrac1b$ car la fonction inverse est strictement décroissante sur $]0\ ; +\infty[$ ;
- si $a < b < 0$ alors $\dfrac{1}{a}>\dfrac{1}{b}$ car la fonction inverse est strictement décroissante sur $]-\infty\ ;\ 0[$.
Résolution d’équations et inéquations à l’aide de la fonction inverse
Résolution d’équations et inéquations à l’aide de la fonction inverse
Exemple
- Résolvons l’équation $\dfrac{1}{x}=2$.
- On trace la représentation de la fonction inverse et la droite d’équation $y=2$ parallèle à l’axe des abscisses.
- On repère ensuite le point d’intersection entre les deux représentations.
- On lit l’abscisse de ce point d’intersection, qui est la solution de l’équation : $S=\{0,5\}$.
Exemple
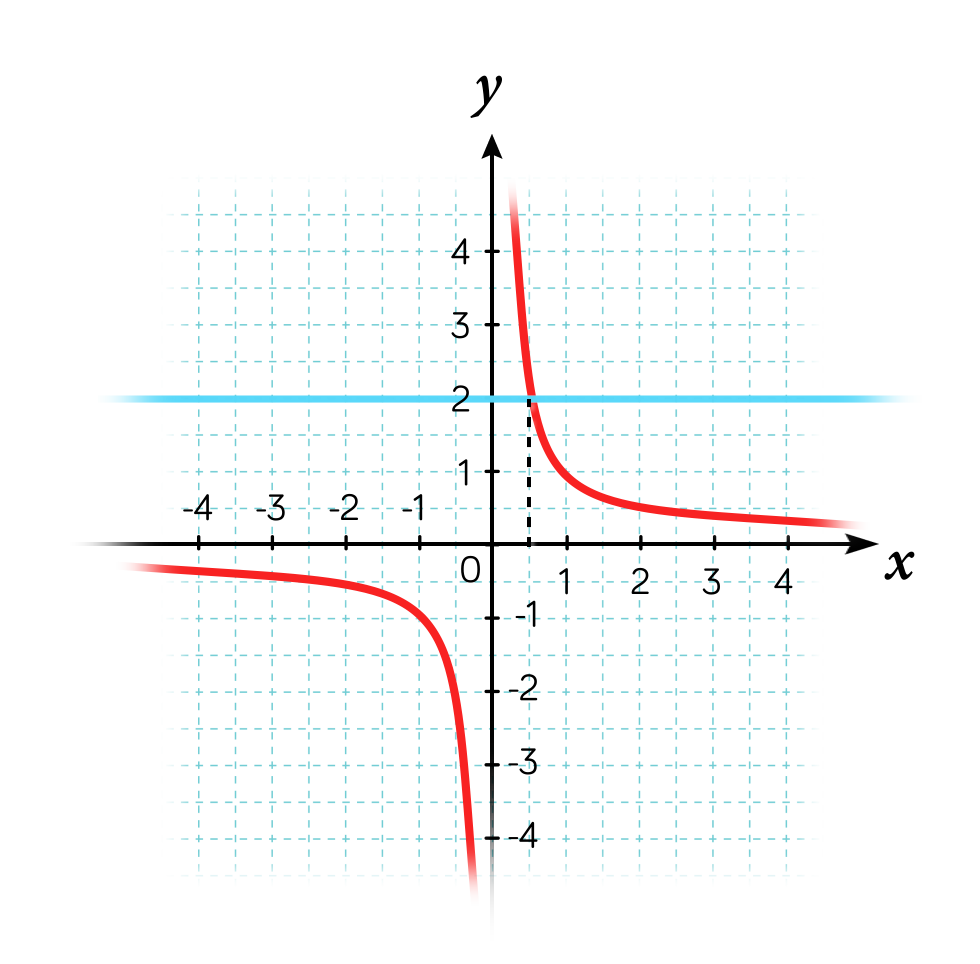
- Résolvons l’inéquation $\dfrac{1}{x}<2$.
- On trace la représentation de la fonction inverse et la droite d’équation $y=2$ parallèle à l’axe des abscisses.
- On repère ensuite le point d’intersection entre les deux représentations.
- On s’intéresse enfin aux abscisses des points de la courbe qui ont une ordonnée strictement inférieure à $2$, l’ensemble de solutions est : $S=]-\infty\ ;\ 0\ [\ \cup\ ]\ 0,5\ ;+\infty[$.
Exemple
- Résolvons l’inéquation $\dfrac{1}{x}\geq2$.
- On trace la représentation de la fonction inverse et la droite d’équation $y=2$ parallèle à l’axe des abscisses.
- On repère ensuite le point d’intersection entre les deux représentations.
- On s’intéresse enfin aux abscisses des points de la courbe qui ont une ordonnée supérieure ou égale à $2$, l’ensemble de solutions est : $S=]\ 0\ ;\ 0,5]$.
