Proportionnalité et pourcentages

Un groupe d’adultes visite un musée pour lequel le tarif d’entrée est de $7$ € par personne.
Nous obtenons le tableau suivant :

Nous avons les égalités suivantes :
$\frac{7}{1} = \frac{14}{2} = \frac{35}{5} = \frac{56}{8} = 7$

Dans ce tableau, on obtient le prix à payer (en €) en multipliant le nombre d’entrées par $7$.

• Il s’agit donc d’un tableau de proportionnalité dont le coefficient de proportionnalité est $7$.

Le tableau suivant indique le prix de paquets de bonbons dans un supermarché.

Ici, nous avons :
$\frac{2,50}{1} = \frac{5}{2} = \frac{7,50}{3} = 2,5$ et $\frac{9}{4} = 2,25 \neq 2,5$

• Le tableau n’est donc pas un tableau de proportionnalité : il y a une réduction pour le quatrième paquet de bonbons acheté.

Une personne achète des tomates dans une épicerie : elles sont vendues $3$ € le kilogramme.
Nous obtenons le tableau suivant :

Nous avons les égalités suivantes :
$\frac{1,50}{0,5} = \frac{3}{1} = \frac{3,60}{1,20} = \frac{4,50}{1,5} = 3$

Dans ce tableau, on obtient le prix à payer (en €) en multipliant la quantité achetée par $3$.

• Il s’agit donc d’un tableau de proportionnalité dont le coefficient de proportionnalité est $3$.

Le tableau suivant indique l’aire d’un carré en fonction de la longueur de son côté.

Nous avons :
$\frac{4}{2} = 2$ ; $\frac{9}{3} = 3$ ; $\frac{16}{4} = 4$ et $\frac{25}{5} = 5$

• Les quotients ne sont pas égaux, le tableau n’est donc pas un tableau de proportionnalité.

On souhaite compléter le tableau de proportionnalité ci-dessous qui indique le montant payé pour un plein d’essence en fonction du nombre de litres d’essence achetés.

Commençons par calculer le coefficient de proportionnalité de ce tableau : $\frac{42}{30} = 1,4$

Cette valeur est le prix au litre de l’essence : pour chaque litre d’essence acheté, on payera $1,40$ €.

On peut ensuite compléter le tableau.

• Pour $10$ litres, on payera $10\times 1,4 = 14$ €.
• Pour $20$ litres, on payera $20\times 1,4 = 28$ €.
• Pour $40$ litres, on payera $40\times 1,4 = 56$ €.
• Pour $50$ litres, on payera $50\times 1,4 = 70$ €.
• Si l’on paye $84$ €, on obtiendra $\frac{84}{1,4} = 60$ litres d’essence.

On obtient donc le tableau de proportionnalité suivant.

On souhaite compléter le tableau de proportionnalité ci-dessous qui indique le montant payé pour des kiwis dans une épicerie. Ils sont vendus $0,60$ € à l’unité.

D’après l’énoncé, le coefficient de proportionnalité de ce tableau est $0,6$.

On peut maintenant compléter le tableau.

• Pour acheter $1$ kiwi, on payera $0,60$ €.
• Pour acheter $2$ kiwis, on payera $2\times 0,6 = 1,20$ €.
• Pour acheter $5$ kiwis, on payera $5\times 0,6 = 3$ €.
• Pour acheter $12$ kiwis, on payera $12\times 0,6 = 7,20$ €.
• Pour $2,40$ €, on obtiendra $\frac{2,40}{0,6} = 4$ kiwis.
• Pour $4,80$ €, on obtiendra $\frac{4,80}{0,6} = 8$ kiwis.

On obtient donc le tableau de proportionnalité suivant.

Un réservoir de voiture de contenance $60\text{ L}$ est plein à $40\ \%$.
Calculons combien il contient de litres d’essence.

$100\ \%$ du réservoir correspondent à $60\text{ L}$.
Nous devons chercher ici à combien de litres correspondent $40\ \%$ du réservoir.

On peut représenter la situation à l’aide d’un tableau de proportionnalité.

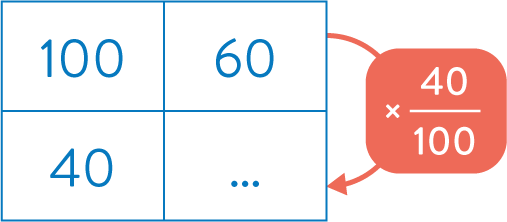
• Le réservoir contient donc $\frac{40}{100} \times 60 = \frac{40\times 60}{100} = \frac{2~400}{100} = 24 \text{ L}$.

Un ordinateur portable a une autonomie de $150$ minutes. Sachant que sa batterie est pleine à $60\ \%$.
Calculons le temps qu’il reste avant que l’ordinateur ne s’éteigne.

• Avant que l’ordinateur ne s’éteigne, il reste $\frac{60}{100} \times 150 = \frac{60\times 150}{100} = \frac{9~000}{100} = 90\text{ min}$.

Dans un collège de $500$ élèves, $25\ \%$ des élèves font du sport en club.
Calculons combien d’élèves de ce collège font du sport en club.

• Le nombre d’élèves de ce collège qui font du sport en club est $\frac{25}{100} \times 500 = 25\times \frac{500}{100} = 25\times 5 = 125$.