burger menuschoolmouv-logo

01 86 76 13 95

(Appel gratuit)

Nos offres
1ere ES
breadcrumb homearrow 1ere ESarrow Mathématiquesarrow

Cours : Second degré

Second degré

Introduction :

Les fonctions polynômes du second degré sont vues pour la première fois en seconde. La première partie de ce cours permet de revoir la définition d’une fonction polynôme de degré 2 ainsi que sa forme canonique et ses variations.

La deuxième partie de cette fiche concerne la résolution d’équations et d’inéquations du second degré. La troisième partie enfin porte sur le signe du trinôme et résolution d’une inéquation du second degré

Fonction polynôme du second degré

Définition

bannière definition

Définition

Fonction polynôme du second degré :

  • Une fonction polynôme de degré $2$ est une fonction définie sur $\mathbb{R}$ dont l’expression algébrique peut être mise sous la forme $f(x)=ax^2+bx+c$ avec $a \ne0$.
  • Les réels $a,\ b$ et $c$ sont appelés coefficients de la fonction polynôme.
  • L’expression $ax^2+bx+c$ est la forme développée de $f(x)$, appelée aussi trinôme du second degré.
bannière exemple

Exemple

La fonction $f(x)=-6x^2+2x +7$ est un polynôme du second degré. Elle est définie sur $\mathbb{R}$. Ses coefficients sont $a=6$ ; $b=2 $ et $c=7$.

Courbes représentatives

bannière propriete

Propriété

Une fonction du type polynôme du second degré aura forcément une parabole comme représentation graphique. Tout comme la fonction carré :

Alt texte

Cependant, toute fonction polynôme du second degré est une fonction carrée qui est multipliée par un réel et/ou additionnée par une fonction affine.

Cette parabole peut donc avoir un décalage vers le haut, vers le bas, vers la droite ou vers la gauche et peut aussi avoir les branches tournées vers le bas, et plus ou moins resserrées :

bannière à retenir

À retenir

Toutes ces variantes se retrouvent par le calcul à l’aide de trois formes d’écritures différentes : la forme développée, la forme canonique et la forme factorisée.

La forme développée

À quoi sert la forme développée ?

La forme développée permet l’identification du degré du polynôme. Attention si le polynôme est de degré autre que 2, tout ce qui est vu dans ce cours n’est pas valable ; la représentation graphique n’est pas une parabole.

Cette forme développée permet de savoir si les branches de la parabole sont tournées vers le haut ou vers le bas:

  • si le coefficient de $x^2$ est positif, alors la parabole a les branches tournées vers le haut (comme la fonction carrée) ;
  • si le coefficient de $x^2$ est négatif, alors la parabole a les branches tournées vers le bas.

Autre utilité de cette forme : on peut connaitre le point d’intersection entre la parabole et l’axe des ordonnées.

La représentation graphique de la fonction $ax^2+bx+c$ avec $a\neq0$ est une parabole qui passe par le point de coordonnées $(0\ ; c)$.

bannière astuce

Astuce

Mais cette forme développée sert aussi à retrouver les autres formes. Il faut trouver la forme développée de l’expression de la fonction polynôme du second degré pour déterminer la forme canonique ou factorisée.

Comment reconnaître et retrouver la forme développée

L’expression $ax^2+bx+c$ avec $a\neq0$ est la forme développée d’une fonction polynôme du second degré appelée aussi trinôme du second degré.

Pour retrouver la forme développée d’une expression, il suffit, comme le dit son nom, de développer l’expression puis de la réduire et enfin l’ordonner.

Par exemple, la fonction $g(x)=(x-1)(2x+3)$

En utilisant la double distributivité, on transforme :

$\begin{aligned}(x)&=(x-1)(2x+3)\\&=2x^2+3x-2x-3\\&=2x^2+x-3\end{aligned}$

On a donc bien la confirmation que cette fonction est du type polynôme du second degré. Sa courbe représentative est une parabole.

Les coefficients du trinôme sont $a=2\;;\ b=1\;;\ c=-3$

Comme $a=2 > 0$ , la parabole a les branches tournées vers le haut. De plus le point d’intersection entre cette parabole et l’axe des ordonnées est le point de coordonnées $(0\ ;-3)$.

La forme canonique

À quoi sert la forme canonique ?

Plusieurs informations découlent de la forme canonique :

  • Premièrement, comme pour la forme développée, tu peux savoir si la parabole a les branches tournées vers le bas ou vers le haut avec le signe de $a$ :

Si $a>0$ la parabole a les branches tournées vers le haut, sinon la parabole a les branches tournées vers le bas.

  • Deuxièmement, on peut lire les coordonnées du sommet $S$ de la parabole : $S\ (\alpha ; \beta)$
  • Troisièmement, avec les deux informations précédentes, on peut établir le tableau de variation de la fonction.

Si $a>0,\ f$ est strictement décroissante sur $]-\infty\ ; \;\alpha]$ puis strictement croissante sur $[\alpha\ ;\ +\infty[$

Si $a<0,\ f$ est strictement croissante sur $]-\infty\ ; \;\alpha]$ puis strictement décroissante sur $[\alpha\ ;\ +\infty[$

  • Quatrièmement, on trouve l’équation de l’axe de symétrie de la parabole : $x=\alpha$
  • Cinquièmement, on connaît l’extremum de la fonction et pour quelle valeur de $x$ il est atteint :

Si $a>0$ alors $f$ admet un minimum $\beta$, atteint en $x=\alpha$

Si $a<0$ alors $f$ admet un maximum $\beta$, atteint en $x=\alpha$

Comment reconnaître et retrouver la forme canonique ?

bannière propriete

Propriété

Toute fonction polynôme de degré 2 (de forme développée $ax^2+bx+c $) admet une écriture de la forme $a(x-\alpha)^2+\beta $ où $\alpha=-\dfrac{b} {2a}$ et $\beta=f (\alpha)$. Cette écriture est la forme canonique de la fonction polynôme.

bannière exemple

Exemple

$f(x)=2x^2+4x-3$

$\begin{aligned}\alpha&=-\dfrac{b}{2a}\\&=-\dfrac{4}{2\times 2}\\&=-\dfrac{4}{4}\\&=-1\end{aligned}$

$\begin{aligned}\beta&=f(\alpha)=f(-1)\\&=2\times(-1)^2+4\times(-1)-3\\&=2-4-3\\&=-5\end{aligned}$

$\begin{aligned}f(x)&= 2(x - (- 1))^2 + (- 5)\\&= 2(x + 1)2 - 5\end{aligned}$

La forme canonique est donc : $f(x) = 2(x + 1)^2 - 5$

La parabole a les branches tournées vers le haut puisque a est positif $(a=2)$.

Le sommet de la parabole a pour coordonnées $(\alpha\ ;\ \beta)$, c’est-à-dire $(-1\ ;\ -5)$ .

Voici le tableau de variation :

La parabole a pour axe de symétrie la droite d’équation $x=\alpha$ c’est-à-dire $x=-1$

Le minimum de la fonction est $-5$ atteint pour $x=-1$

La forme factorisée

À quoi sert la forme factorisée

bannière à retenir

À retenir

La forme factorisée permet de :

  • savoir si la parabole a les branches tournées vers le bas ou vers le haut avec le signe de $a$ ;
  • savoir combien de fois la courbe coupe l’axe des abscisses ;
  • calculer les abscisses des points d’intersection entre la courbe et l’axe des abscisses ;
  • résoudre les équations et les inéquations ;
  • connaître le signe du polygone ;
  • établir le tableau des signes.

Comment reconnaître et retrouver la forme factorisée

bannière definition

Définition

Équation du second degré :

  • une équation du second degré, d’inconnue $x$, est une équation qui peut s’écrire sous la forme $ax^2+bx+c=0$ où a, b et c sont des nombres réels donnés, avec $a\neq0$.
  • Une solution de cette équation est appelée racine du trinôme $ax^2+bx+c$.
bannière propriete

Propriété

Pour résoudre une équation du type $ax^2+bx+c=0$, on calcule tout d’abord le discriminant $\Delta$ du trinôme $ax^2+bx+c $ :

$\Delta=b^2-4ac$

  • Si $\Delta>0$, alors l’équation $ax^2+bx+c=0$ admet deux solutions distinctes :

$x_1=\dfrac{-b-\sqrt{\Delta}} {2a}$

et

$x_2=\dfrac{-b+\sqrt {\Delta}}{2a}$

  • Si $\Delta=0$, alors l’équation $ax^2+bx+c=0$ admet une unique solution :

$x_0=-\dfrac{b}{2a}$

  • Si $\Delta<0$, alors l’équation $ax^2+bx+c=0$ n’a pas de solution.

bannière exemple

Exemple

  • Résoudre l’équation $-5x^2-9x+2=0$

$\begin{aligned}\Delta&=b^2-4ac\\&=(-9)^2-4\times(-5)\times2\\&=81+40=121\end{aligned}$

Comme $\Delta $ est strictement positif, l’équation admet deux solutions distinctes :

$\begin{aligned}x_1&=\dfrac{-b-\sqrt{}\Delta}{2a}\\&=\dfrac{9-\sqrt{121}}{2\times(-5)}\\&=\dfrac{9-11}{-10}\\&=\dfrac{-2}{-10}\\&=\dfrac{1}{5}\end{aligned}$

$\begin{aligned}x_2&=\dfrac{-b+\sqrt{}\Delta}{2a}\\&=\dfrac{9+\sqrt{121}}{2\times(-5)} \\&=\dfrac{9+11}{-10} \\&=\dfrac{20}{-10}\\&=-2\end{aligned}$

Donc $S={-2\dfrac{1}{5}}$

  • Résoudre l’équation $\dfrac{1}{3}x^2-2x +3=0$

$\begin{aligned} \Delta&=b^2-4ac\\ &=(-2)^2-4\times\dfrac{1}{3}\times3\\ &=4-4\\ \Delta&=0 \end{aligned}$

Comme $\Delta $ est nul, l’équation admet une unique solution :

$\begin{aligned}x_0&=-\dfrac{b}{2a}\\&=-\dfrac{(-2)}{2\times\dfrac{1}{3}}\\&=\dfrac{2}{\dfrac{2}{3}}\\&=2\times\dfrac{3}{2}\\&=3\end{aligned}$

Donc $S=3$

  • Résoudre l’équation $3x^2-x+2=0$

$\begin{aligned} \Delta&=b^2-4ac\\ &=(-1)^2-4\times3\times2\\ &=1-24\\ \Delta&=-23 \end{aligned}$

Comme $\Delta $ est strictement négatif, l’équation n’admet pas de solution.

Donc $S=\varnothing$

bannière astuce

Astuce

Le symbole $\varnothing$ se lit « ensemble vide »

Factorisation du trinôme

bannière propriete

Propriété

Soit $f(x)=ax^2+bx+c$ avec $a\ne0$, un trinôme du second degré :

Si le discriminant du trinôme est strictement positif ($\Delta>0$), $f(x)=a(x-x_1)(x-x_2)$ où $x_1$ et $x_2$ sont les racines du trinôme.

Si le discriminant du trinôme est strictement nul ($\Delta=0$), $f(x)=a(x-x_0)^2$où $x_0$ est la racine du trinôme.

Si le discriminant du trinôme est strictement négatif ($\Delta<0$), alors $f(x)$ ne se factorise pas.

bannière exemple

Exemple

  • Le trinôme $-5x^2-9x+2$ admet pour racines le couple $S=\left\lbrace-2\ ;\dfrac{1}{5}\right\rbrace$; la forme factorisée est donc :

$\begin{aligned}a(x-x_1)(x-x_2)&=-5\Big(x-\big(-2\big)\Big)\Big(x-\dfrac{1}{5}\Big)\\&=-5(x+2)\Big(x-\dfrac{1}{5}\Big)\end{aligned}$

  • Le trinôme $\dfrac{1}{3}x^2-x+3$ avait une unique racine $S=3$ ; la forme factorisée est donc :

$a(x-x_0)^2=\dfrac{1}{3}(x-3)^2$

  • Le trinôme $3x^2-x+2$ n’a aucune racine. Il n’existe donc pas de forme factorisée.

Signe du trinôme et résolution d’une inéquation du second degré

Signe du trinôme

bannière astuce

Astuce

Faire attention de bien ranger les racines dans l’ordre croissant dans la première ligne des tableaux de signes.

bannière propriete

Propriété

On considère le trinôme du second degré $ax^2+bx+c$:

Dans le cas où $\Delta>0$, le trinôme est du signe de $a$ sur $]-\infty\ ;\ x_1[$ et sur $]x_2\ ;\ +\infty[$ et du signe contraire de $a$ sur $]x_1\ ;\ x_2[$.

Dans le cas où $\Delta=0$, le trinôme est du signe de $a$ pour tout réel $x\ne x_0$ et le trinôme s’annule pour $x=x_0$.

Dans le cas où $\Delta<0$, pour tout réel $x$, le trinôme est du signe de $a$.

bannière exemple

Exemple

  • Étudier le signe de $-5x^2-9x+2$ sur $\mathbb{R}$

Le trinôme $-5x^2-9x+2$ admet pour racines le couple $S=\left\lbrace-2\ ;\dfrac{1}{5}\right\rbrace$, de plus $a=-5 < 0$ donc le trinôme est négatif à l’extérieur des racines ; ce qui donne le tableau de signes suivant :

  • Étudier le signe de $\dfrac{1}{3}x^2-x+3$ sur $\mathbb{R}$

Le trinôme $\dfrac{1}{3}x^2-x+3$ admet pour racine unique $S={3}$, de plus $a=\dfrac{1}{3}>0$ donc le trinôme est positif pour tout $x\ne 3$ ; ce qui donne le tableau de signes suivant :

  • Étudier le signe de $3x^2-x+2$ sur $\mathbb{R}$

Le trinôme $3x^2-x+2$ n’a aucne racine, de plus $a=3>0$ donc le trinôme est positif pour tout réel $x$ ; ce qui donne le tableau de signes suivant :

Résolution d’inéquations du second degré

bannière à retenir

À retenir

En construisant un tableau de signes il est possible de résoudre n’importe quelle inéquation du second degré.

bannière exemple

Exemple

  • Résoudre l’inéquation $-5x^2-9x+2\geq0$

Pour résoudre cette inéquation, on utilise le tableau de signes correspondant, on regarde sur quel intervalle le trinôme est positif et on note l’ensemble solution : $S=[-2\ ;\dfrac{1}{5}]$.

  • Résoudre l’inéquation $3x^2-x+2<0$

De même, pour résoudre $3x^2-x+2<0$, on utilise le tableau de signes correspondant on voit qu’il n’existe aucun intervalle où le trinôme est négatif et on note l’ensemble de solution : $S=\varnothing$.

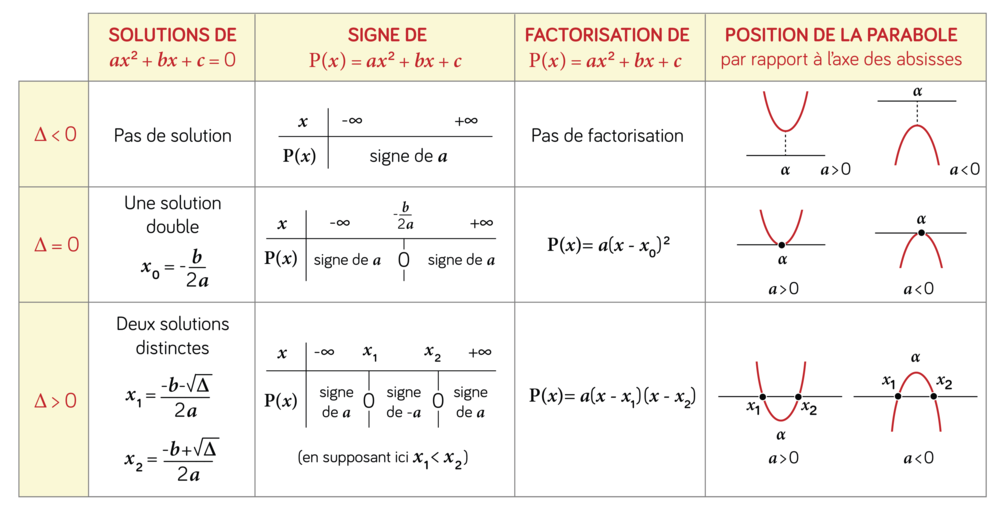
Conclusion :

Ce tableau récapitulatif permet de mémoriser comment résoudre une équation ou une inéquation du second degré et comment factoriser un trinôme, dans tous les cas possibles.