Cours : Sections planes
Sections planes
Introduction :
Dans ce cours, nous allons parler des sections planes des principaux solides dans l’espace. Nous aborderons d’abord quelques définitions et propriétés puis nous verrons les cas pratiques de ces sections.
Astuce
Une section plane est la surface produite par l’intersection d’un solide et d’un plan.
Lorsque l’on coupe un solide par un plan, la surface de coupe obtenue s’appelle la section plane du solide.
Section d’un pavé droit par un plan
Section d’un pavé droit par un plan
Propriété
Propriété 1
La section d’un pavé droit par un plan $P$ parallèle à une face est un rectangle identique à cette face.
Propriété
Propriété 2
La section d’un pavé droit par un plan $P$ parallèle à une arête est un rectangle.
Astuce
En résumé, lorsque le plan de coupe est parallèle à une face ou à une arête, la section d’un pavé droit est toujours un rectangle.
Section d’un cylindre de révolution par un plan
Section d’un cylindre de révolution par un plan
Propriété
Propriété 1
La section d’un cylindre de révolution de rayon $R$ par un plan $P$ parallèle aux bases est un disque de rayon $R$.
Propriété
Propriété 2
La section d’un cylindre de révolution par un plan $P$ parallèle à son axe est un rectangle.
Astuce
En résumé, lorsque le plan de coupe est parallèle ou perpendiculaire à l’axe de révolution d’un cylindre, la section est selon le cas un rectangle ou un disque.
Section d’une pyramide par un plan
Section d’une pyramide par un plan
Propriété
La section d’une pyramide à base polygonale par un plan $P$ parallèle à la base est un polygone ayant la même forme que la base.
Section d’un cône de révolution par un plan
Section d’un cône de révolution par un plan
Propriété
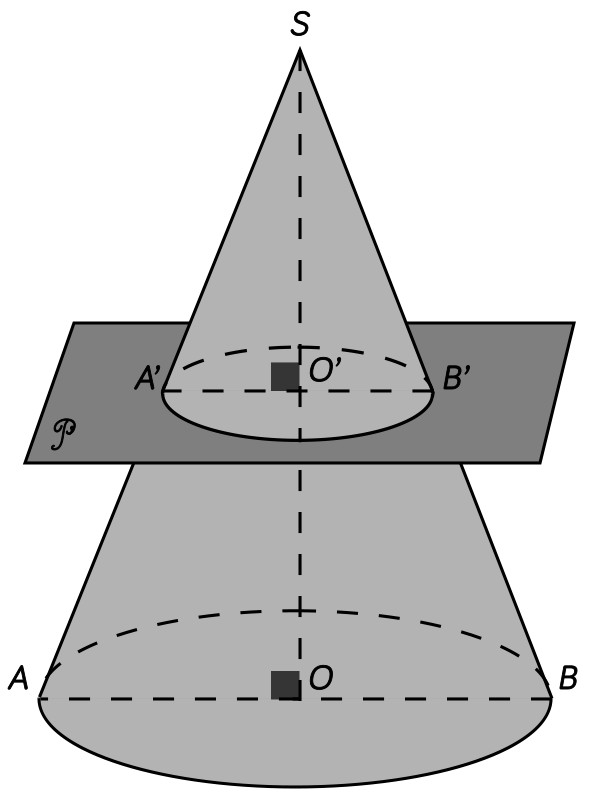
La section d’un cône de révolution par un plan $P$ parallèle à la base est un cercle dont le centre appartient à la hauteur du cône.
Astuce
En géométrie il est important, voire primordial, de connaître les propriétés qui lient les solides, notamment toutes celles sur les aires et volumes abordées dans les cours précédents.