[IN] Introduction : La trigonométrie est abordée dès le collège où l’on étudie le cosinus en 4^^e^^ puis le sinus et la tangente en 3^^e^^. Nous allons donc poursuivre le travail en découvrant tout d’abord le cercle trigonométrique puis l’enroulement de la droite des réels autour de ce cercle. Nous verrons ensuite les définitions et propriétés du cosinus et du sinus d’un nombre réel, nous ferons le lien avec la trigonométrie dans le triangle rectangle et nous observerons les valeurs remarquables des cosinus et sinus. [/IN] ##Cercle trigonométrique et droite des réels/1 ###Cercle trigonométrique/a. [DEF] **Cercle trigonométrique :** Dans le plan muni d’un repère orthonormé $(O,\ I,\ J)$ le cercle trigonométrique est le cercle $\mathcal{C}$ de centre $O$ et de rayon 1 orienté dans le sens inverse des aiguilles d’une montre. [/DEF] [RETENIR] Le sens direct d’orientation est aussi appelé sens **trigonométrique** ou sens **positif**. [IMG]((35))![](https://images.schoolmouv.fr/mathematiques-2nde-cours6-trigonometrie-img01.png) #[/IMG] Le sens indirect (négatif) est donc celui des aiguilles d’une montre. * $I$ est le point de coordonnées $(1\ ;0)$ * $J$ est le point de coordonnées $(0\ ;1)$ [/RETENIR] ###Enroulement de la droite des réels sur le cercle trigonométrique/b. Dans un repère orthonormé $(O,\ I,\ J)$ on considère le cercle trigonométrique et la droite $(d)$ tangente au cercle au point $I$. La droite $(d)$ est donc parallèle à $(OJ)$. [IMG]![](https://images.schoolmouv.fr/mathematiques-2nde-cours6-trigonometrie-img02.png) #[/IMG] On imagine que la droite $(d)$ s’enroule autour du cercle. Les deux propriétés suivantes permettent de comprendre comment est « gradué » le cercle trigonométrique. [PROP] Pour tout réel $a$, le point d’abscisse $a$ sur $(d)$ coïncide avec un unique point du cercle trigonométrique $M$. $M$ s’appelle l’image de $a$. [/PROP] [PROP] **Réciproque :** Réciproquement, à tout point $M$ du cercle trigonométrique correspond une infinité de valeurs qui peuvent être considérées comme les abscisses des points de la droite $(d)$. Si $a$ est l’abscisse d’un de ces points sur $(d)$ tous les autres points de $(d)$ d’image $M$ ont pour abscisse $a+2\pi,\ a+4\pi,\ …\ ,\ a-2\pi,\ a-4\pi,\ … $ c’est-à-dire tous les réels de la forme $a+2k\pi$ avec $k$un entier relatif. Comme à chaque réel $a$ on associe un point $M$ sur le cercle trigonométrique. $a$ est lié à l’angle au centre $\widehat{IOM}$. Ceci permet de définir une nouvelle unité d’angle appelée radian. [/PROP] [EX] Si le point $M$ est placé en $J$, alors l’angle $\widehat{IOM}$ mesure $ \dfrac{\pi}{2}$ radians. Voilà ce que donne le cercle trigonométrique lorsqu’on y place les principales valeurs de $a$ : [/EX] [IMG]((50))![](https://images.schoolmouv.fr/mathematiques-2nde-cours6-trigonometrie-img03.png) #[/IMG] ##Cosinus et sinus d’un nombre réel/2 ###Définitions et propriétés/a. [DEF] **Cosinus :** Soit $M$ le point du cercle trigonométrique associé à un réel $a$. Le cosinus du réel $a$, noté $\cos a$, est l’abscisse du point $M$ dans le repère $(O,\ I,\ J)$. [/DEF] [DEF] **Sinus :** Soit $M$ le point du cercle trigonométrique associé à un réel $a$. Le sinus du réel $a$, noté $\sin a$, est l’ordonnée du point $M$ dans le repère $(O,\ I,\ J)$. [/DEF] [IMG]((50))![](https://images.schoolmouv.fr/mathematiques-2nde-cours6-trigonometrie-img04.png) #[/IMG] * Ainsi, à chaque réel $a$, on peut associer une unique valeur du cosinus et du sinus.((fleche)) * Le point $M$ a pour coordonnées $M(\cos a\ ;\sin a)$.((fleche)) [EX] Le réel $\dfrac{\pi}{2}$ a pour image le point $J$ de coordonnées $(0\;;1)$. * Donc $\cos \dfrac{\pi}{2}=0$ et $\sin \dfrac{\pi}{2}=1$.((fleche)) [/EX] [PROP] Pour tout nombre réel $x$ on a : $\begin{aligned} &-1\leq \cos x\leq1\\ &-1\leq \sin x\leq1\\ \end {aligned}$ [/PROP] [PROP] Pour tout nombre réel $x$ on a : $(\cos x)^2+(\sin x)^2=1$ Ce qui peut se noter : $\cos^2x+\sin^2x=1$ [/PROP] [RETENIR] Lorsque l’on connaît $\sin x$ et que l’on cherche $\cos x$ ou inversement, on doit utiliser la relation fondamentale $(\cos x)^2+(\sin x)^2=1$ [/RETENIR] [EX] On donne $\sin x=0,8$ et $0< x <\dfrac{\pi}{2}$ Le but est de trouver la valeur de $\cos x$ : $\begin{aligned}&\cos^2x+\sin^2x=1 \\&\Leftrightarrow\cos^2x+(0,8)^2=1\\ &\Leftrightarrow\cos^2x+0,64=1\\ &\Leftrightarrow\cos^2x=1-0,64\\ &\Leftrightarrow\cos^2x=0,36\\ &\Leftrightarrow\cos x=\sqrt{0,36}\text{ ou }\cos x=-\sqrt{0,36}\\ &\Leftrightarrow\cos x=0,6\text{ ou }\cos x=-0,6\\ \end{aligned}$ L’énoncé dit que $x$ est compris entre $0$ et $\dfrac{\pi}{2}$ donc il se situe sur le quart de cercle en haut à droite et son cosinus est donc positif. * On en déduit que $\cos x=0,6$.((fleche)) [/EX] ###Lien avec la trigonométrie dans le triangle rectangle/b. [IMG]((50))![](https://images.schoolmouv.fr/mathematiques-2nde-cours6-trigonometrie-img05.png) #[/IMG] * Dans le triangle rectangle $OBM$ on a : $\cos \widehat{BOM}=\dfrac{\text{côté adjacent}}{\text{hypoténuse}}=\dfrac{OB}{OM}$ Or $OM$ est un rayon du cercle trigonométrique donc $OM=1$. D’où $\cos \widehat{BOM}=\dfrac{OB}{1}=OB=\cos x$ * On retrouve la même valeur pour $\cos x$ avec le cercle trigonométrique que pour $\cos \widehat{BOM}$ avec la trigonométrie dans le triangle rectangle.((fleche)) * De même, dans le triangle rectangle $OBM$ on a : $\sin \widehat{BOM}=\dfrac{\text{côté opposé}}{\text{hypoténuse}}=\dfrac{BM}{OM}=\dfrac{OC}{OM}$ Or $OM$ est un rayon du cercle trigonométrique donc $OM=1$. D’où $\sin \widehat{BOM}=\dfrac{OC}{1}=OC=\sin x$ * On retrouve la même valeur pour $\sin x$ avec le cercle trigonométrique que pour $\sin \widehat{BOM}$ avec la trigonométrie dans le triangle rectangle.((fleche)) ###Valeurs remarquables des cosinus et sinus/c. Les valeurs remarquables des cosinus et sinus sont regroupées dans ce tableau : [IMG]![](https://images.schoolmouv.fr/mathematiques-2nde-cours6-trigonometrie-img09.png) #[/IMG] On voit par exemple en vert dans le tableau que le cosinus de $\pi\over6$ vaut $\sqrt{3}\over2$ et que le sinus de $\pi\over6$ vaut $1\over2$. [ATT] Ces valeurs sont à connaître par cœur car elles permettent de déduire les valeurs du cosinus et du sinus d’autres angles de la même famille comme par exemple $5\pi\over6$. 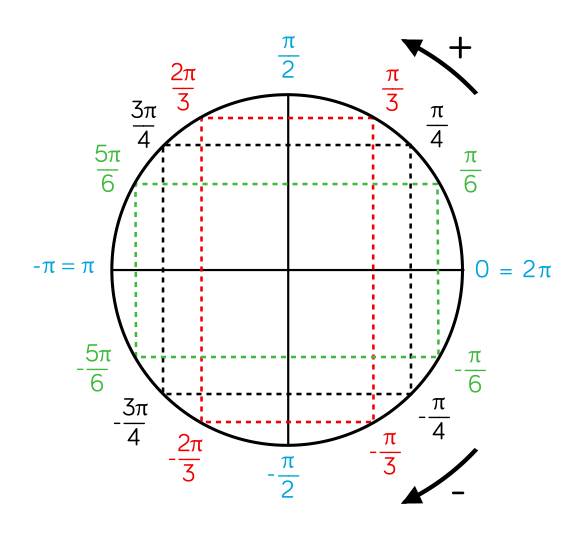[/ATT] [IMG]![](https://images.schoolmouv.fr/mathematiques-2nde-cours6-trigonometrie-img07.png) #[/IMG] Dans le cercle trigonométrique ci-dessus, on a représenté en rouge les points associés à $\dfrac{\pi}{3};-\dfrac{\pi}{3};\dfrac{2\pi}{3};-\dfrac{2\pi}{3}$. * On remarque par exemple que le cosinus de $\dfrac{2\pi}{3}$ est opposé au cosinus de $\dfrac{\pi}{3}$ mais que le sinus de $\dfrac{2\pi}{3}$ est égal au sinus de $\dfrac{\pi}{3}$.((fleche)) En vert les points associés à $\dfrac{\pi}{6};-\dfrac{\pi}{6};\dfrac{5\pi}{6};-\dfrac{5\pi}{6}$ en noir $\dfrac{\pi}{4};-\dfrac{\pi}{4};\dfrac{3\pi}{4};-\dfrac{3\pi}{4}$ et en bleu $0 ;\dfrac{\pi}{2};-\dfrac{\pi}{2};\pi$. [AST] Apprendre le cercle trigonométrique par cœur sera très utile de savoir convertir les degrés en radians et inversement. [/AST] [RETENIR] Formule de conversion des degrés en radians : $180\degree= \pi\ \text{radians}$ Pour effectuer une conversion, il suffit d’utiliser la proportionnalité. [/RETENIR] [EX] [IMG]![](https://images.schoolmouv.fr/mathematiques-2nde-cours6-trigonometrie-img08.png) #[/IMG] [/EX]