Cours : Vergence, image, grandissement et relation de conjugaison

Distance focale et formule de vergence

Rappels sur la représentation des systèmes optiques

Dans le cours précédent, nous avons vu qu’une lentille peut être convergente ou divergente. Quelque soit son effet, elle possède un centre optique, que l’on nomme généralement $\text O$.

Pour étudier le comportement des rayons lumineux passant par une lentille, on la représente sur un axe orienté dans le sens conventionnel de propagation de la lumière. Cet axe est l’axe optique ; il passe par le centre optique $\text O$.

De part et d’autre du point $\text O$, se trouvent les foyers. Le foyer image est noté $\text F'$, son symétrique par rapport à $\text O$ est le foyer objet, on le note $\text F$.

La distance entre le centre optique et le foyer image s’appelle la distance focale image.

Distance focale image et formule de vergence

Définition

​Distance focale image :

La distance focale image est la mesure algébrique de la distance entre le centre optique et le foyer image. On la note $f'$ et on a : $f'=\overline{\text {OF'}}$.

La distance focale image $f'$ est positive pour une lentille convergente et négative pour une lentille divergente.

Astuce

La barre horizontale au dessus de $\text{OF'}$ signifie « mesure algébrique ». C’est en fait la longueur qui sépare $\text O$ de $\text F'$.

La distance focale image permet de déterminer la vergence de la lentille. C’est ce que mesurent les ophtalmologues et les opticiens pour déterminer la correction nécessaire en cas de troubles de la vision.

Définition

Vergence d’une lentille :

La vergence est une grandeur qui exprime la capacité d’une lentille à faire converger les faisceaux lumineux qu’elle reçoit. Elle est égale à l’inverse de la distance focale image : $V=\dfrac{1}{f'}$

L’unité de la vergence $V$ est le $\text m^{-1}$ ou la dioptrie $(\delta)$. L’unité de $f'$ est le mètre $(\text m)$.

À partir de la formule générale, on peut obtenir les expressions suivantes : $V\times f'=1$ et $f'=\dfrac{1}{V}$

Tracer l’image d’un objet

Rayons particuliers

Avant de pouvoir tracer l’image d’un objet par une lentille convergente, il faut tracer les rayons incidents particuliers.

Rappel

On dit « incident » pour parler d’un faisceau qui arrive dans le système optique. En sortie de système optique, on parle de faisceau émergeant.

Pour en revenir aux rayons particuliers, on les appelle comme cela parce qu’on connaît la déviation qu’ils subissent en traversant une lentille (qu’elle soit convergente ou divergente).

Propriété

Propriétés physiques des rayons particuliers :

Il existe trois rayons particuliers :

• Les rayons qui passent par le centre optique ne subissent aucune déviation ; pour les représenter, il suffit de prolonger le rayon incident :

Rayons particuliers non déviés par une lentille

• Les rayons incidents parallèles à l’axe optique donnent des rayons émergents dirigés vers le foyer image :

Rayons incidents particuliers parallèles à l’axe optique et convergeant vers le foyer image

• Les rayons émergents parallèles à l’axe optique sont issus de rayons incidents qui passent par le foyer objet :

Rayons émergeants particuliers parallèles à l’axe optique et convergeant vers le foyer objet

Image réelle

Rappel

Le fond de l’œil, c’est-à-dire la rétine, est assimilé à un écran. En optique, l’écran est l’emplacement du système où l’image se forme.

Définition

Image réelle :

L’image d’un objet est réelle :

• si elle se situe après la lentille et qu’elle peut être observée sur un écran ;
• si l’objet est situé avant le foyer objet de la lentille.

Pour tracer l’image réelle d’un objet correspondant à un segment $\text{[AB]}$ perpendiculaire à l’axe optique et dont le point $\text A$ appartient à cet axe, le principe est le suivant :

• l’image $\text A'\text B'$ d’un objet $\text{AB}$ perpendiculaire à l’axe optique est aussi perpendiculaire à l’axe optique ;
• on construit le point image $\text B'$ du point $\text B$, puis le point image $\text A'$ du point $\text A$.

On trace ensuite le comportement des rayons lumineux particuliers :

• pour obtenir le point image $\text B'$ du point $\text B$ il faut tracer deux rayons incidents particuliers partant du point $\text B$ : celui qui passe par le centre optique et celui qui est parallèle à l’axe optique. Le point image $\text B'$ se situe à l’intersection des deux rayons émergents.
• pour obtenir le point image $\text A'$ du point $\text A$, il faut tracer la perpendiculaire à l’axe optique passant par le point $\text B'$. Le point $\text A'$ se trouve à l’intersection de cette perpendiculaire et de l’axe optique.

Image virtuelle

Définition

Image virtuelle :

En optique, un objet a une image virtuelle si elle ne peut pas être observée sur un écran : un observateur doit se placer directement derrière la lentille pour voir cette image.

Propriété

Propriété de l’image virtuelle :

On obtient une image virtuelle lorsque l’objet est situé entre le foyer objet et le centre optique.

Pour tracer l’image virtuelle d’un objet correspondant à un segment $\text{[AB]}$ perpendiculaire à l’axe optique et dont le point $\text A$ appartient à cet axe :

• L’image $\text A'\text B'$ d’un objet $\text{AB}$ perpendiculaire à l’axe optique est aussi perpendiculaire à l’axe optique. On construit le point image $\text B'$ du point $\text B$, puis le point image $\text A'$ du point $\text A$.
• Pour obtenir le point image $\text B'$ du point $\text B$, il faut tracer deux rayons incidents particuliers partant du point $\text B$ : celui qui passe par le centre optique et celui qui est parallèle à l’axe optique. Il faut ensuite prolonger les deux rayons émergents correspondants (en pointillés). Le point $\text B'$ est situé à l’intersection de ces deux rayons émergents.
• Notons que, connaissant la position de $\text B'$, on peut alors tracer un troisième rayon particulier, celui qui émerge parallèlement à l’axe optique.
• Pour obtenir le point image $\text A'$ du point $\text A$, il faut tracer la perpendiculaire à l’axe optique passant par $\text B'$. $\text A'$ se situe à l’intersection de cette perpendiculaire et de l’axe optique.

Cas particulier d’image : le plan focal

Dans le cas particulier d’un objet situé à l’infini, l’objet image se situe dans le plan focal image. Et réciproquement, dans le cas particulier d’un objet situé dans le plan focal objet, l’objet image se forme à l’infini.

En optique, tout objet éloigné est considéré comme étant situé à l’infini.

Définition

Plan focal image et plan focal objet :

Le plan focal image est un plan perpendiculaire à l’axe optique et passant par le foyer image.

Le plan focal objet est un plan perpendiculaire à l’axe optique et passant par le foyer objet.

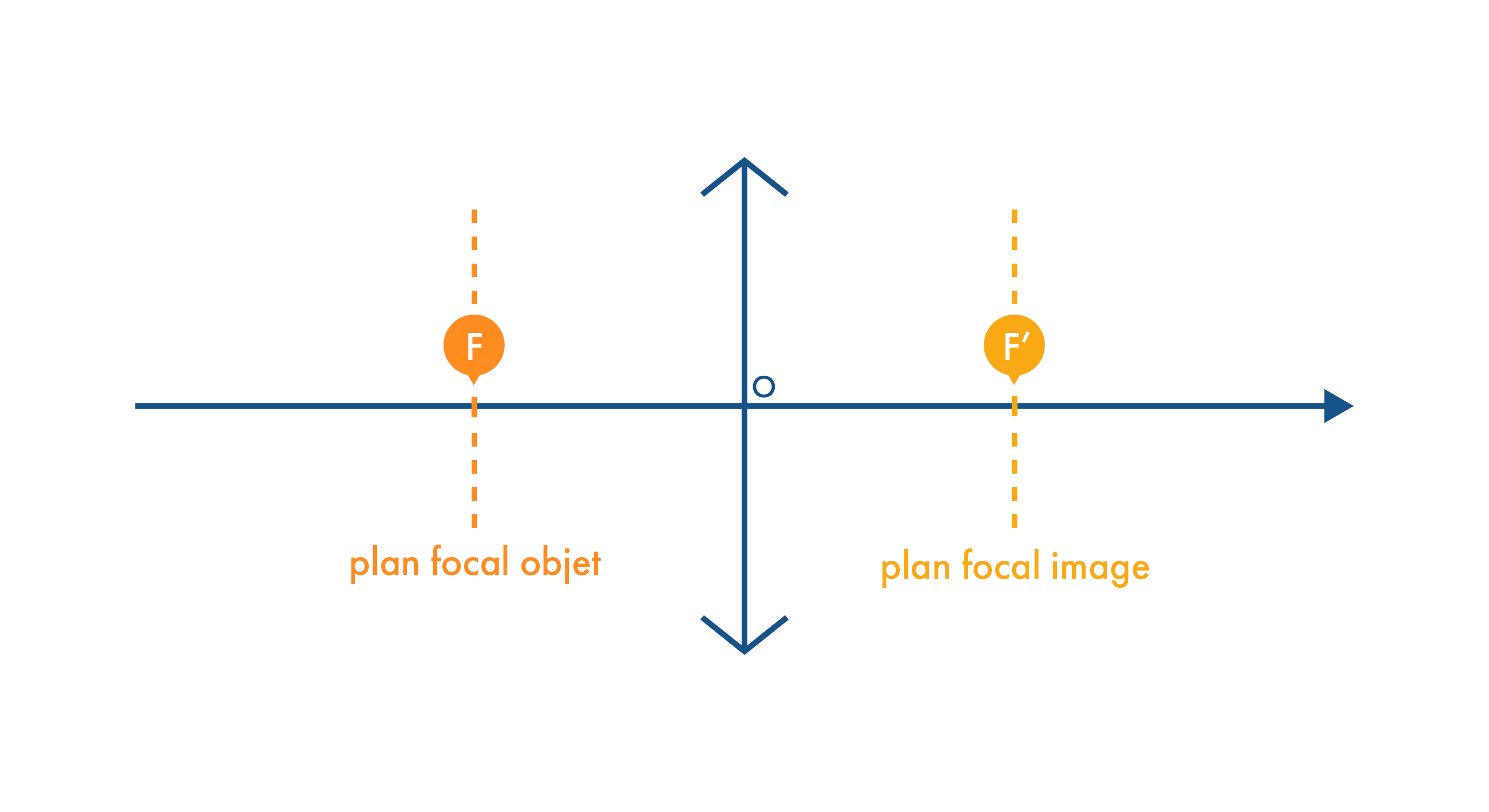Emplacement du plan focal objet et du plan focal image

Relation de conjugaison

Conventions

Comme l’axe optique est orienté suivant le sens de propagation de la lumière (de gauche à droite) on peut associer aux longueurs des segments un signe en utilisant la notation algébrique.

Ainsi, une mesure algébrique sera positive si elle est dans le sens de la propagation de la lumière et négative dans le cas contraire.

Dans cet exemple $\text{OA}$ est négatif et $\overline{\text{OA'}}$ est positif.

Relation de conjugaison

Définition

Relation de conjugaison :

La relation de conjugaison permet de déterminer la position de l’image d’un objet quand la position de l’objet et la distance focale image de la lentille sont connues.

Si le point $\text A'$ est l’image d’un point objet $\text A$ par une lentille de centre optique $\text O$ et de foyer image $\text F'$ alors la relation de conjugaison donne : $$\dfrac{1}{\text{OA'}}-\dfrac{1}{\text{OA}}=\dfrac{1}{\text{OF'}}$$

Grandissement

Définition

Grandissement d’une lentille :

À partir de la relation de conjugaison on peut déterminer le grandissement d’une lentille :

$\gamma=\dfrac{\overline{\text{A'B'}}}{\overline{\text{AB}}}=\dfrac{\overline{\text{OA'}}}{\overline{\text{OA}}}$

Le grandissement se note avec la lettre grecque $\gamma$ (gamma). C’est une mesure sans dimension et sans unité.

• Si $\gamma$ est positif alors l’image s’inscrit dans le même sens que l’objet. Si $\gamma$ est négatif, l’image de l’objet est renversée.
• Si la valeur absolue de $\gamma$ est supérieure à 1 alors l’image est plus grande que l’objet. Le grandissement d’une lentille permet de comparer la taille de l’image à celle de l’objet.